By Jacob D. Bekenstein
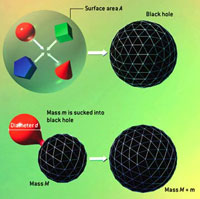 Image: ALFRED T. KAMAJIAN |
THE THERMODYNAMICS OF BLACK HOLES allows one to deduce limits on the density of entropy or information in various circumstances.
The holographic bound defines how much information can be contained in a specified region of space. It can be derived by considering a roughly spherical distribution of matter that is contained within a surface of area A. The matter is induced to collapse to form a black hole (a). The black hole's area must be smaller than A, so its entropy must be less than A/4 [see illustration]. Because entropy cannot decrease, one infers that the original distribution of matter also must carry less than A/4 units of entropy or information. This result--that the maximum information content of a region of space is fixed by its area--defies the commonsense expectation that the capacity of a region should depend on its volume.
The universal entropy bound defines how much information can be carried by a mass m of diameter d. It is derived by imagining that a capsule of matter is engulfed by a black hole not much wider than it (b). The increase in the black hole's size places a limit on how much entropy the capsule could have contained. This limit is tighter than the holographic bound, except when the capsule is almost as dense as a black hole (in which case the two bounds are equivalent).
The holographic and universal information bounds are far beyond the data storage capacities of any current technology, and they greatly exceed the density of information on chromosomes and the thermodynamic entropy of water (c).